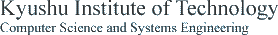研究室の研究協力者である，槙 孝一郎 さんが，数理モデルによる新型コロナウィルスの東京の第４波についての一考察を述べていますので，共有させて頂きます．

　首都東京の感染者数累計は2020年4月中旬から一定の倍率で伸びている。図1は，東京都の感染者数であるが，対数軸での直線の傾きは0.011で、それは月に1.4倍の増加になる。もし、この傾向が2021年4月から2か月間続くならば、3月末日で12万人の累計が6月初めには2倍の24万人になると推定される。1年前の感染者と最近の感染者は全く異なるのに増加傾向が一定であることは、東京都民は1年間、同じ生活様式を守り続けていることを意味する。



　この間に、第2、第3の波があったが、この増加傾向に影響は少ない。小さな揺れは、あたかも大きな野火の延焼中に燃えやすい枯草の山を巻き込んだように見える。東京都の厳しい自粛生活一偏の中でも、一定の割合で感染率の高い揺らぎ（枯草集団）があれば、各種キャンペーンや年末休暇中の行動とは関係なしに、それが燃えただけといえる。もちろん延焼最前線での行動変化は傾きに大きな影響を与えるはずである。

　
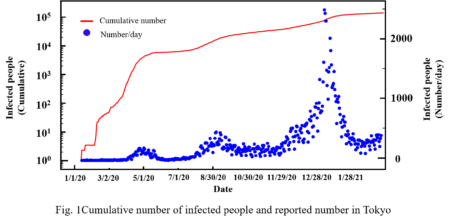
　今後、本当のコロナ抑制の期待は、2021年3月から続く図の直線の傾きが0.011以下で維持されることである。しかし、図2に示す全国都道府県の感染者数累計を見るとその期待は薄れる。東京都 、大阪府 、・・・・、 沖縄県の上位9県はそれぞれの第１波発生後、東京と同じ傾きで増
加している。たとえ感染者数の少ない県であっても、累計数の平らな時期を経て、枯草に火が付いたように感染者急増があり、結局、東京都と同じ増加傾向がうかがえる。したがって、東京都の累計者数グラフが4月以降に平らになったとしても、その後急激な感染拡大が発生し、この指数関数的増加傾向は続く可能性がある。



　感染のSIR数理モデルでは未感染者数S=(回復率γ）/(感染率β）になったときが増加のピークなので、γ=0.1(人/日)として指数をβーγ=0.011とみなせば、感染者累計が全体の10％になるまで傾斜は緩まない。

また，感染拡大への飲食店の影響を数理モデルで考えてみました。

　新規感染者が指数関数的に増大することを感染拡大といいますが、これは、毎日、感染者数に比例して感染が鼠算で伝搬するからです。この比例係数が数理モデルでは感染率（実際は、感染率ー回復率）です。飲食店で様々な感染対策を施していますが、ほとんどが感染率を下げることに対応します。感染率が下がるだけでは、鼠算になる数理モデルのままです。感染率が回復率より下がれば収束しますが、実際に感染が起こっている飲食店の感染率が問題なので、全体の平均感染率が下がっても効果は期待できません。そもそも感染拡大は感染者数の急増ですから、その感染を起こさせ、場所も同じ数だけ急増しているはずです。飲食店以外もこの感染場所拡大に油を注いでいす。そうなると対策は、この増加する連鎖を切ることであり、すべての場所の感染率を下げることはではないはずです。

　逆に感染対策をしていない飲食店の影響を考えてみると、毎日入店者総数以下の感染者を出すだけで、指数関数的増加にはなりえません。感染者が新しい飲食店へ次から次へと入っていくことが感染拡大の原因です。この原因を抑えずに飲食店の時間短縮をしても効果は数理モデル的に期待できません。感染者の「感染確率のある場所へ」の往来を止めるべきです。「感染確率のあるところ」となるとスーパー、病院など例外を作らずに人が集まるところすべてです。感染者だけのロックダウンです。

　この感染者の入店を防ぐには、どうすべきでしょうか。感染者は感染を受けた時と広げる時と2回感染確率のある場所を訪れています。しかも2回目は発症中です。もし、発症が感染4日後で、回復が10日後だとすると、一度どこか感染確率のあるところに入店したら、すべて感染者とみなして4日後から10日までは他の店も含め入店しないことです。これは感染の可能性のある人を仮想感染者としてしまうことに相当します。PCR検査して陰性であれば、リセットです。このような対策で、発症前4日間の人々の入店により飲食店は通常営業が可能です。「もし感染が判明したら徹底的に追跡調査される」条件が入店時に必要かも。

———————–

槙さんは，数理モデルの専門家ですが，このような感染状況も数理モデルで説明できるのに驚きました．
読めば読むほど，納得できますし，とても分かり易い説明かと思います．
とても興味深い考察です．